摘要:多项式(FFT,NTT),生成函数
FFT
引入
设:
$$
\begin{split}
A=\sum_{i=0}^{n} a_ix^i \\
B=\sum_{i=0}^{m} b_ix^i
\end{split}
$$
那么:
$$
\begin{split}
C&=A\ast B\\
&=\sum_{i=0}^{nm}\sum_{j=0}^{i}a_jb_{i-j}x^{i}
\end{split}
$$
时间复杂度 $O(n^2)$,无法接受,考虑优化。
前置
单位根
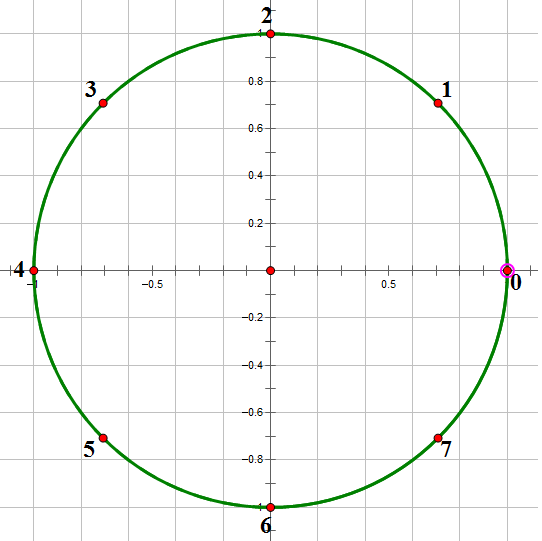
在复平面上画一个以 $(0,0)$ 为圆心的圆,将圆 $n$ 等分,并规定 $(1,0)$ 为第零个等分点,逆时针标号,就得到了第 $0$ 到 $n-1$ 个等分点,也就是第 $0$ 到 $n-1$ 个 $n$ 次单位根,记做 $\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$ 。
性质 :
$\omega_n^k=e^\frac{2\pi ik}{n}$
$e^{i\theta}=cos\theta+i\ast sin\theta$
$\omega_{dn}^{dk}=\omega_n^k$
$\omega_{dn}^{dk}=e^\frac{2\pi idk}{dn}=e^\frac{2\pi ik}{n}=\omega_n^k$
$\omega_n^k=a+bi \Rightarrow \omega_n^{-k}=a-bi$
$\omega_n^k=e^\frac{2\pi ik}{n}$
$\omega_n^{k+\frac n2}=-\omega_n^k$
$\omega_n^{k+\frac n2}=\omega_n^k\ast \omega_n^\frac n2=-\omega_n^k$
DFT
DFT 主要的思想是在求一部分值的时候求出来另外一部分,然后分治进行。
比如说我们要求 $A(x)=\sum_{i=0}^{n} a_ix^i$ 在 $x_1,x_2,\cdots,x_n$ 处取值,那么:
将 $A$ 的系数按照下标的奇偶性分类,即:
$$
\begin{split}
A_0(x)&=a_0+a_2x^1+a_4x^2+\cdots \\
A_1(x)&=a_1+a_3x^1+a_5x^2+\cdots \\
A(x)&=A_0(x^2)+x\ast A_1(x^2)
\end{split}
$$
分别将 $\omega_n^k$ 和 $\omega_n^{k+\frac{n}{2}}$ 代入得:
$$
\begin{cases}
A(\omega_n^k)&=&A_0(\omega_{n/2}^{k})+\omega_n^kA_1(\omega_{n/2}^k)\\
A(\omega_n^{k+\frac n2})&=&A_0(\omega_{n/2}^{k})-\omega_n^{k}A_1(\omega_{n/2}^{k})
\end{cases}
$$
递归求解,时间复杂度 $O(n\log n)$
IDFT
IDFT 可以看作是 DFT 的逆运算。
先引入单位根的一个性质:
$$
\dfrac1n\sum_{i=0}^{n-
1}\omega_n^{v\ast i}=[v\bmod n=0]
$$
其实很好证明:
$$
\begin{split}
&\because\omega_{n}^{v\ast i}=\omega_{n}^{v\ast i}\ast \omega_{n}^{v}\\
&\therefore {\omega_n^{v\ast i}}\ \text is\ 等比数列\\
&1.\ v\bmod n=0\\
&\ \ \ \sum_{i=0}^{n-1}\omega_n^{v\ast i}=\sum_{i=0}^{n-1} 1^i=n\\
&2.\ v\bmod n\not=0\\
&\ \ \ \sum_{i=0}^{n-1}\omega_n^{v\ast i}=\dfrac{1-\omega_n^{n\ast v}}{1-\omega_n^v}=\dfrac{1-1^v}{1-\omega_n^v}=0
\end{split}
$$
假设我们要求 $C=A\ast B$ :
$$
\begin{split}
c_i=&\sum_{j=0}^{i-1}a_j\times b_{i-1-j}\\
c_i=&\sum_{p=0}\sum_{q=0}a_p\times b_q\left[(p+q-i)\bmod n=0\right] \\
nc_i=&\sum_{p=0}\sum_{q=0}a_p\times b_q\sum_{j=0}\omega_n^{(p+q-i)j}\\
nc_i=&\sum_{j=0}\omega_n^{(-i)j}(\sum_{p=0}\omega_n^{pj}a_p)(\sum_{q=0}\omega_n^{qj}b_q)
\end{split}
$$
设:
$$
f_a(j)=\sum_{i=0}\omega_n^{ji}a_i\ ,\ f_a^{-1}(j)=\sum_{i=0}\omega_n^{(-j)i}a_i
$$
然后:
$$
{\begin{split}
nc_i=&\sum_{j=0}\omega_n^{(-i)j}f_a(j)f_b(j)\\
nc_i=&\sum_{j=0}\omega_n^{(-i)j}f_c(j)\\
nc_i=&f_{f_c}^{-1}(i)
\end{split}}
$$
唯一的坑点在于
maxn的取值,一开始没注意,1e6+6=> WA(read '-')+ RE,2e6+6还是 WA,最后3e6+6AC !
#include<bits/stdc++.h>
using namespace std;
typedef long double ldb;
const int maxn = 3e6+6;
const ldb Pi = acos(-1.0);
int n, m, q = 1;
int a[maxn], b[maxn], c[maxn];
struct Complex {
ldb x, y;
friend Complex operator + (Complex a, Complex b) {return {a.x+b.x, a.y+b.y};}
friend Complex operator - (Complex a, Complex b) {return {a.x-b.x, a.y-b.y};}
friend Complex operator * (Complex a, Complex b) {return {a.x*b.x-a.y*b.y, a.x*b.y+a.y*b.x};}
} x1[maxn], x2[maxn];
void change(Complex x[], int len) {
for (int i=1, j=len/2, k; i < len-1; i++) {
if (i < j) swap(x[i], x[j]);
k = len / 2;
while (j >= k) j -= k, k /= 2;
j += k;
}
}
void FFT(Complex x[], int len, int im) {
change(x, len);
for (int d = 1; d <= len; d <<= 1) {
Complex wn = {cos(Pi * 2 / d), sin(im * 2 * Pi / d)};
for (int j = 0; j < len; j += d) {
Complex w = {1, 0};
for (int k = j; k < j + d / 2; k++) {
Complex u = x[k], t = w * x[k + d / 2];
x[k] = u + t;
x[k + d / 2] = u - t;
w = w * wn;
}
}
}
if (im == -1)
for (int i = 0; i < len; i++)
x[i].x /= len;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 0; i <= n; i++) scanf("%d", &a[i]), x1[i]={(ldb)a[i], 0};
for (int i = 0; i <= m; i++) scanf("%d", &b[i]), x2[i]={(ldb)b[i], 0};
while(q <= (n + m + 2)) q <<= 1;
FFT(x1, q, 1), FFT(x2, q, 1);
for (int i = 0; i < q; i++) x1[i] = x1[i] * x2[i];
FFT(x1, q, -1);
for (int i = 0; i < q; i++) c[i] = (int)(x1[i].x + 0.5);
q = n + m;
for (int i = 0; i <= q; i++) printf("%d ", c[i]); puts("");
return 0;
}
NTT
在某些时候,我们需要求模 $p$ 意义下的卷积
先求出 $p$ 的原根 $g$,方法如下
从小到大枚举 $d\in [2,p-1]$,令 $a_i$ 为 $\varphi(p)$ 的素因子,若 $d^{\frac{\varphi(p)}{a_i}}\equiv1\pmod p$ 都不成立,那么 $d$ 就是模 $p$ 的一个原根
这种方法的证明:
假设对于 $d^{\frac{\varphi(p)}{a_i}}\equiv1\pmod p$ 均不成立,但存在 $k<\varphi(p)$,使得 $dk\equiv1\pmod p$
令 $q=\gcd(k,\varphi(p))$,那么 $q<p$ 并且 x 一定整除 $\dfrac{\varphi(p)}{a_i}$ 中的一个,不妨设它整除 $\dfrac{\varphi(p)}{a_i}$
考虑等式 $kn+\varphi(p)m=q$,容易发现一定存在正整数解
由于 $d^q\equiv d^{kn+φ(p)m}≡1\pmod p$,而 $q|\dfrac{\varphi(p)}{a_i}$,与假设矛盾
得证
在求出原根后,可以发现,$g^\frac{p-1}n$ 与 $w_n$ 的性质类似
所以我们可以用 $g^\frac{p-1}n$ 来代替 $w_n$
和FFT几乎相同
PS:这种方法只在 $p=a*2^k+1$ 的情况下才成立
三模数 NTT
首先挑选 3 个 $a*2^k+1$ 形式的模数,进行3次 NTT,求出3组答案
然后将每一个数用中国剩余定理合并即可
生成函数
普通生成函数
定义
序列 $a$ 的普通生成函数为:
$$
F(x)=\sum_{n}a_{n}x^{n}
$$
换句话说,如果序列 a 有通项公式,那么它的普通生成函数的系数就是通项公式。
运算
$$
\begin{split}
F(x)\pm G(x)=\sum_n (a_n\pm b_n)x^n
\\
F(x)G(x)=\sum_n x^n \sum_{i=0}^na_ib_{n-i}
\end{split}
$$
封闭形式
例如 $\left<1,1,1,\dots\right>$ 的普通生成函数为:$F(x)=\sum_{n\ge 0}x^{n}$
因为:
$$
F(x)x+1=F(x)
$$
所以:
$$
F(x)=\frac{1}{1-x}
$$
推导
- $a=\left<0,1,1,1,\dots\right>$
$$
F(x)=\sum_{n\ge 1}x^n=
$$