[机器学习] 学习笔记 贰 训练不起来怎么办

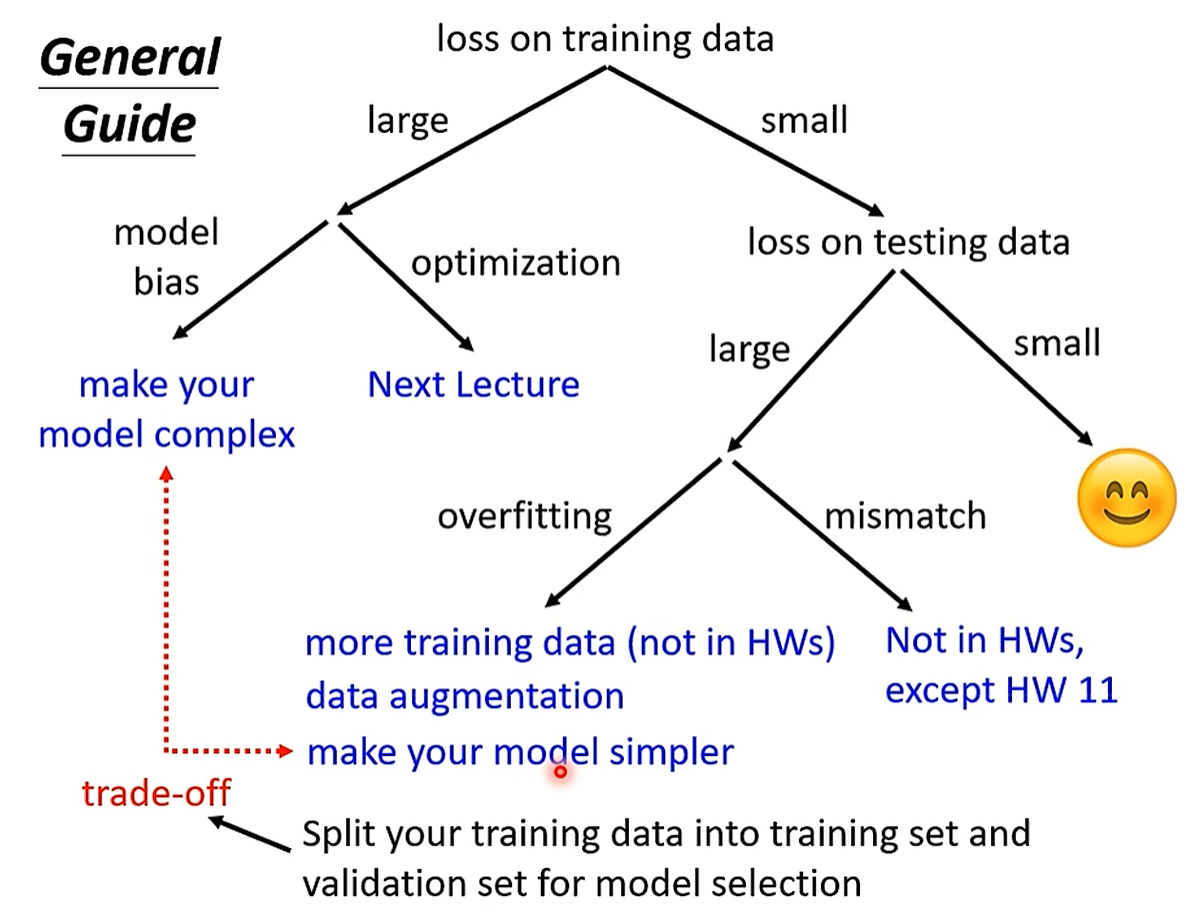
Model Bias

Problem: The model is too simple.

Solution: Redesign you model to make it more flexible.

More features or Deep Learning (more neurons, layers)

Optimization

Critical point (gradient is close to 0): Local minima / Saddle point

$H$: Hessian Matrix

$$L(\boldsymbol\theta)\approx L(\boldsymbol\theta')+\frac{1}{2}(\boldsymbol\theta-\boldsymbol\theta')^{T}H(\boldsymbol\theta-\boldsymbol\theta')$$

记 $\boldsymbol v^THv=\frac{1}{2}(\boldsymbol\theta-\boldsymbol\theta')^{T}H(\boldsymbol\theta-\boldsymbol\theta')$

• Local minima:

  For all $\boldsymbol v$, $\boldsymbol v^THv>0\to \text{Around } \boldsymbol\theta':L(\boldsymbol\theta)>L(\boldsymbol\theta')$

  $H$ is positive definite = All eigen values are positive.

• Local maxima:

  For all $\boldsymbol v$, $\boldsymbol v^THv<0\to \text{Around } \boldsymbol\theta':L(\boldsymbol\theta)<L(\boldsymbol\theta')$

  $H$ is negative definite = All eigen values are negative.

• Saddle point:

  Sometimes $\boldsymbol v^THv>0$, Sometimes $\boldsymbol v^THv<0$

  Some eigen values are positive, and some are negative.

error surface 维度很高，因此 local minima 很少。

Model Bias v.s. Optimization Issue

e.g. 56-layer 比 20-layer 更差，不是 overfitting，而是 optimization issue。

建议：先使用简单的 model，不容易出现 optimization issue，

Overfitting

An extreme example:

$$f(\boldsymbol x)= \begin{cases} \hat y^i & \exist\boldsymbol x^i=\boldsymbol x\\ \text{random} & \text{otherwise} \end{cases}$$

Solution:

• More training data

• Data augumentation

  e.g. 图像识别：左右翻转，缩放，但不应该上下翻转

• Constrained model

  • Less parameters, sharing parameters (CNN)

  • Less features

  • Early stopping

  • Regularization 正则化

  • Dropout

Batch

• Large batch: long time for cooldown, but powerful

• Samll batch: short time for cooldown, but noisy

因为有 GPU 平行运算（显存换时间），所以跑一个 epoch，large batch update 的次数更少，更有效率

Warning: Large batch size 容易出现 optimization fails

	Samll	Large
Speed for one update (no parallel)	Faster	Slower
Speed for one update (with parallel)	Same	Same(not too large)
Time for one epoch	Slower	Faster
Gradient	Nosiy	Stable
Optimization	Better	Worse
Generalization	Better	Worse

Momentum

Learning Rate

震荡，Loss 不再减少，但是 Gradient 不为 0

Learning rate 要为每一个参数客制化

$$\theta_i^{t+1}\leftarrow\theta_i^t-\eta g_i^t, g_i^t=\frac{\partial L}{\partial \theta_i}|_{\theta=\theta^t}$$

$$\theta_i^{t+1}\leftarrow\theta_i^t-\frac{\eta}{\sigma_i^t} g_i^t$$

Adagrad

Root Mean Square 均方根

$$\theta_i^{1}\leftarrow\theta_i^0-\frac{\eta}{\sigma_i^0} g_i^0,\ \sigma_i^0=\sqrt{(g_i^0)^2}=|g_i^0|\\\\ \theta_i^{2}\leftarrow\theta_i^1-\frac{\eta}{\sigma_i^1} g_i^1,\ \sigma_i^1=\sqrt{\frac{1}{2}[(g_i^0)^2 + (g_i^1)^2]}\\\\ \dots\\\\ \theta_i^{t+1}\leftarrow\theta_i^t-\frac{\eta}{\sigma_i^t} g_i^t,\ \sigma_i^t=\sqrt{\frac{1}{t+1}\sum_{j=0}^t(g_i^j)^2}$$

RMSProp

$0<\alpha<1$

$$\theta_i^{1}\leftarrow\theta_i^0-\frac{\eta}{\sigma_i^0} g_i^0,\ \sigma_i^0=\sqrt{(g_i^0)^2}\\\\ \theta_i^{2}\leftarrow\theta_i^1-\frac{\eta}{\sigma_i^1} g_i^1,\ \sigma_i^1=\sqrt{\alpha(\sigma_i^0)^2 + (1-\alpha)(g_i^1)^2}\\\\ \dots\\\\ \theta_i^{t+1}\leftarrow\theta_i^t-\frac{\eta}{\sigma_i^t} g_i^t,\ \sigma_i^t=\sqrt{\alpha(\sigma_i^{t-1})^2 + (1-\alpha)(g_i^t)^2}$$

Adam: RMSProp + Momentum

Learning Rate Scheduling

$$\theta_i^{t+1}\leftarrow\theta_i^t-\frac{\eta^t}{\sigma_i^t} g_i^t$$

Learning Rate Dacay

递减

Warm Up

先增大再减小