摘要:多项式全家桶
前置
单位根
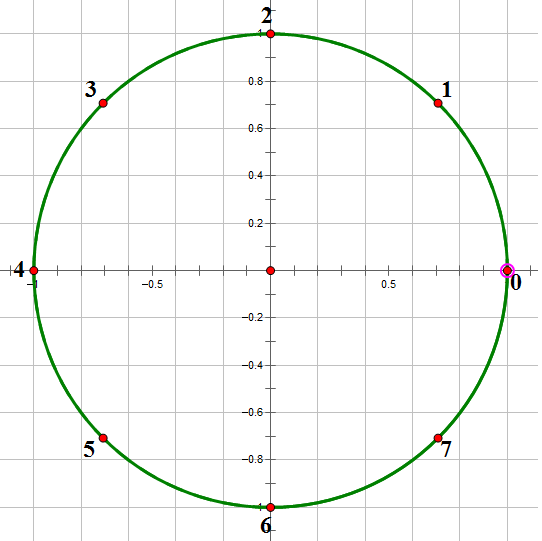
在复平面上画一个以 $(0,0)$ 为圆心的圆,将圆 $n$ 等分,并规定 $(1,0)$ 为第零个等分点,逆时针标号,就得到了第 $0$ 到 $n-1$ 个等分点,也就是第 $0$ 到 $n-1$ 个 $n$ 次单位根,记做 $\omega_n^0,\omega_n^1,\cdots,\omega_n^{n-1}$ 。
性质 :
$\omega_n^k=e^\frac{2\pi ik}{n}$
$e^{i\theta}=cos\theta+i\ast sin\theta$
$\omega_{dn}^{dk}=\omega_n^k$
$\omega_{dn}^{dk}=e^\frac{2\pi idk}{dn}=e^\frac{2\pi ik}{n}=\omega_n^k$
$\omega_n^k=a+bi \Rightarrow \omega_n^{-k}=a-bi$
$\omega_n^k=e^\frac{2\pi ik}{n}$
$\omega_n^{k+\frac n2}=-\omega_n^k$
$\omega_n^{k+\frac n2}=\omega_n^k\ast \omega_n^\frac n2=-\omega_n^k$
$
\dfrac1n\sum_{i=0}^{n-
1}\omega_n^{v\ast i}=[v\bmod n=0]
$证明:
$$\begin{split}
&\because\omega_{n}^{v\ast i}=\omega_{n}^{v\ast i}\ast \omega_{n}^{v}\
&\therefore {\omega_n^{v\ast i}}\ \text is\ 等比数列\
&1.\ v\bmod n=0\
&\ \ \ \sum_{i=0}^{n-1}\omega_n^{v\ast i}=\sum_{i=0}^{n-1} 1^i=n\
&2.\ v\bmod n\not=0\
&\ \ \ \sum_{i=0}^{n-1}\omega_n^{v\ast i}=\dfrac{1-\omega_n^{n\ast v}}{1-\omega_n^v}=\dfrac{1-1^v}{1-\omega_n^v}=0
\end{split}$$
导数
常数和基本初等函数导数公式:
$$\begin{aligned}
(C)’ &= 0\
(x^\mu)’ &= \mu x ^{\mu-1}\
(\sin x)’ &= \cos x\
(\cos x)’ &= -\sin x\
(a^x)’ &= a^x ; \ln a (a > 0, a \not= 1)\
(e^x)’ &= e^x\
(\log _a x)’ &= \frac{1}{x \ln a} ; (a > 0, a \not= 1)\
(\ln x)’ &= \frac{1}{x}
\end{aligned}$$
复合函数的求导法则:
定理 1: 如果 $u = g(x)$ 在点 $x$ 可导,$y = f(u)$ 在点 $u = g(x)$,那么复合函数 $y = f(g(x))$ 在点 $x$ 可导,且其导数为 $\frac{\operatorname{d}y}{\operatorname{d}x} = f’(u) \cdot g’(x)$ 或 $\frac{\operatorname{d}y}{\operatorname{d}x} = \frac{\operatorname{d}y}{\operatorname{d}u} \cdot \frac{\operatorname{d}u}{\operatorname{d}x}$。
积分
定义 1: 如果在区间 $\mathbf{I}$ 上,可导函数 $F(x)$ 的导数为 $f(x)$,即 $\forall x \in \mathbf{I}$,都有 $F’(x) = f(x)$ 或 $\operatorname{d}F(x) = f(x)\operatorname{d}x$
那么函数 $F(x)$ 就称为 $f(x)$ 或 $f(x)\operatorname{d}x$ 在区间 $\mathbf{I}$ 上的一个原函数。
原函数存在定理:连续函数一定有原函数
定义 2: 在区间 $\mathbf{I}$ 上,函数 $f(x)$ 的带有任意常数项的原函数称为 $f(x)$(或 $f(x)\operatorname{d}x$) 在区间 $\mathbf{I}$ 上的不定积分,记作 $\int f(x)\operatorname{d}x$。
其中,记号 $\int$ 称为积分号,$f(x)$ 称为被积函数, $f(x)\operatorname{d}x$ 称为被积表达式,$x$ 称为积分变量。
Taylor 展开
泰勒中值定理 1: 如果函数在 $x_0$ 处有 $n$ 阶导数,那么存在 $x_0$ 的一个邻域,对于该邻域内任一 $x$,有
$f(x) = f(x_0) +f’(x_0)(x-x_0) + \frac{f’’(x_0)}{2!} (x-x_0)^2+…+\frac{f^{(n)}(x_0)}{n!}(x-x_0)^n + R_n(x)$
其中,$R_n(x) = \omicron((x-x_0)^n)$.
泰勒展开在 $x_0$ 处展开的封闭形式如下: $\sum\limits_{n=0}^{+\infty} \frac{f^{(n)}(x_0)}{n!}(x-x_0)^n$
Newton 迭代
牛顿迭代用于求函数零点,通过不断地切线逼近所求值,但最终也只是近似值,迭代的次数越多,精确度越高,误差越小。
若我们要求函数 $f(x)$ 的零点,初始近似值为 $x_0$,切线方程为 $y = f’(x_0) (x - x_0) + f(x_0)$
令 $y = 0$,得 $x = x_0 - \frac{f(x_0)}{f’(x_0)}$.
还需提的一点是,在多项式中,每迭代一次,精度翻倍。
多项式乘法
引入
设:
$$
\begin{split}
A=\sum_{i=0}^{n} a_ix^i \
B=\sum_{i=0}^{m} b_ix^i
\end{split}
$$
那么:
$$
\begin{split}
C&=A\ast B\
&=\sum_{i=0}^{nm}\sum_{j=0}^{i}a_jb_{i-j}x^{i}
\end{split}
$$
时间复杂度 $O(n^2)$,无法接受,考虑优化。
快速 Fourier 变换
$$
\begin{aligned}
f_k &=\sum_{i = 0}^{n-1} \omega_n^i g_i\
g_k &=\frac{1}{n}\sum_{i = 0}^{n-1} \omega_n^{-i} f_i
\end{aligned}
$$
离散 Fourier 变换
DFT 主要的思想是在求一部分值的时候求出来另外一部分,然后分治进行。
比如说我们要 求 $A(x)=\sum_{i=0}^{n} a_ix^i$ 在 $x_1,x_2,\cdots,x_n$ 处取值,那么:
将 $A$ 的系数按照下标的奇偶性分类,即:
$$
\begin{split}
A_0(x)&=a_0+a_2x^1+a_4x^2+\cdots \
A_1(x)&=a_1+a_3x^1+a_5x^2+\cdots \
A(x)&=A_0(x^2)+x\ast A_1(x^2)
\end{split}
$$
分别将 $\omega_n^k$ 和 $\omega_n^{k+\frac{n}{2}}$ 代入得:
$$
\begin{cases}
A(\omega_n^k)&=&A_0(\omega_{n/2}^{k})+\omega_n^kA_1(\omega_{n/2}^k)\
A(\omega_n^{k+\frac n2})&=&A_0(\omega_{n/2}^{k})-\omega_n^{k}A_1(\omega_{n/2}^{k})
\end{cases}
$$
递归求解,时间复杂度 $O(n\log n)$
离散 Fourier 逆变换
IDFT 可以看作是 DFT 的逆运算。
先引入单位根的一个性质:
我们有一个多项式:
$$A(x) = \sum_{i = 0}^{n-1}a_i x^i$$
将 $n$ 个单位根代入得到 $n$ 个点值,$\omega_n^i$ 对应的点值记为 $y_i$。
令 $B(x)=\sum\limits_{i = 0}^{n-1}y_i x^i$ ,将 $\omega_n^k$ 的倒数(共轭复数)$\omega_n^{-k}$ 代入:
$$\begin{aligned}
B(\omega_n^{-k})
&=
\sum_{i = 1} ^{n-1} y_i \omega_n^{-ik}
\
&=
\sum_{i = 0}^{n-1}
\left(
\sum_{j = 0}^{n-1} a_j \omega_n^{ij}
\right)
\omega_n^{-ik}
\
&=
\sum_{j = 0}^{n-1}
a_j
\sum_{i = 0}^{n-1}
\left(
\omega_n^{j-k}
\right)^i
\
&=
n a_k
\
\therefore a_k &= \frac{B(\omega_n^{-k})}{n}
\end{aligned}
$$
快速数论变换
快速数论变换
在某些时候,我们需要求模 $p$ 意义下的卷积
先求出 $p$ 的原根 $g$,方法如下
从小到大枚举 $d\in [2,p-1]$,令 $a_i$ 为 $\varphi(p)$ 的素因子,若 $d^{\frac{\varphi(p)}{a_i}}\equiv1\pmod p$ 都不成立,那么 $d$ 就是模 $p$ 的一个原根
这种方法的证明:
假设对于 $d^{\frac{\varphi(p)}{a_i}}\equiv1\pmod p$ 均不成立,但存在 $k<\varphi(p)$,使得 $dk\equiv1\pmod p$
令 $q=\gcd(k,\varphi(p))$,那么 $q<p$ 并且 x 一定整除 $\dfrac{\varphi(p)}{a_i}$ 中的一个,不妨设它整除 $\dfrac{\varphi(p)}{a_i}$
考虑等式 $kn+\varphi(p)m=q$,容易发现一定存在正整数解
由于 $d^q\equiv d^{kn+φ(p)m}≡1\pmod p$,而 $q|\dfrac{\varphi(p)}{a_i}$,与假设矛盾
得证
在求出原根后,可以发现,$g^\frac{p-1}n$ 与 $w_n$ 的性质类似
所以我们可以用 $g^\frac{p-1}n$ 来代替 $w_n$
和FFT几乎相同
PS:这种方法只在 $p=a*2^k+1$ 的情况下才成立
快速数论逆变换
在 IDFT 中,我们将单位根的倒数(共轭复数)代入上文的多项式 $B(x)$ 中得到转换后的系数,而在 INTT 中代入的则是原根在模 $p$ 意义下的逆元。
任意模数快速数论变换
在 NTT 中,模数是有要求的,是质数并且能写成 $a\cdot2^k+1$ 的形式。
比如:
$$
\begin{aligned}
469762049 &= 7\ast 2^{26}+1 \
998244353 &= 119\ast 2^{23}+1 \
1004535809&= 479\ast 2^{21}+1
\end{aligned}
$$
而 $2^k$ 则是 NTT 能够运算的最大长度。
对于题目要求的其他模数,比如 $10^9+7$,或者普通的 NTT 就显得心有余而力不足了。
任意模数 NTT(也可以称作三模数 NTT)在众望中出世。
我们知道: FFT 的运算结果 $\leq N P ^2$, 所以我们可以找三个大质数相乘大于这个结果,对三个模数分别计算出结果,最后中国剩余定理合并,然后模提莫要求的模数即可。
当然,直接合并这么大的数是会 Bomb 的,我们可以先合并前两个,再使用一些神奇的操作求出答案。
记最终答案为 $ans$, 选择的三个质数分别为 $p_1, p_2, p_3$,
记三次 NTT 的结果为:
$$
\begin{aligned}
ans\equiv a_1\pmod{p_1}\
ans\equiv a_2\pmod{p_2}\
ans\equiv a_3\pmod{p_3}
\end{aligned}
$$
先用 CRT 合并得到:
$$
ans \equiv a_4 \pmod {p_1 p_2}
$$
转化为等式为:
$$
ans = k p_1 p_2 + a_4
$$
若求出 $k$ 便可得到 $ans$:
$$
\begin{aligned}
\because ans &\equiv a_3 &\pmod{ p_3}\
\therefore k p_1 p_2 + a_4 &\equiv a_3 &\pmod {p_3}\
\therefore k &\equiv (a_{3}-a_{4}) p_1^{-1} p_2^{-1} &\pmod{p_3}\
\therefore ans &\equiv k p_1 p_2 + x_4 &\pmod{p_1 p_2 p_3}
\end{aligned}
$$
因为 $ans$ 是小于 $p_1 p_2 p_3$ 的,所以$ans = k p_1 p_2 + x_4$。(别忘记取模)
分治快速数论变换
假设有一个形式为 f[i]=∑j=1if[i−j]g[j]
它显然不是卷积,但是差别仅在于等号的右侧也出现了 f
处理方法类似 CDQ 分治
假设现在已经求出了 f(0) 到 f(n2),要计算它们对未知部分 f(n2+1) 到 f(n) 的贡献
发现一个已知的 f(x),对任意一个 f(i)(i>x) 的贡献都只有 f(x)g(i-x)
于是贡献函数 F 就长这样了:
F(x)=∑xi=1f(i)g(x−i)
其中 f 只填充 [l,mid] 的部分,因为其他地方的 f=0
g 只填充 [1,r−l] 的部分,因为只算对于 [mid,r] 的贡献
多项式乘法逆
定义多项式 $F^{-1}$ 为 多项式 $F$ 的乘法逆元,满足
$$
F \ast F^{-1} \equiv 1 \pmod {x^n}
$$
若我们已经得知 $F \ast H \equiv 1 \pmod {n^\frac{n}{2}}$,需要我们求 $F \ast G \equiv 1 \pmod {n^2}$。
首先,$F \ast G \equiv 1 \pmod {n^{\frac{n}{2}}}$ 也是成立的,接下来就是推式子的时间:
主要思想是递归处理,每次减半
首先我们在 modxn 处的逆元可以费马小定理直接求
现在假设我们现在求出来了 F∗G≡1(modx⌈n2⌉) , 要
求 F∗G′≡0(modxn)
那么
$$
\begin{aligned}G’&\equiv G&&\pmod {x^{\lceil\frac n2\rceil}}\(G’-G)^2&\equiv0&&\pmod {x^n}\F*(G’-G)^2&\equiv0&&\pmod {x^n}\FG’^2-2FGG’+FG^2&\equiv0&&\pmod {x^n}\G’-2G+FG^2&\equiv0&&\pmod {x^n}\G’&\equiv 2G-FG^2&&\pmod {x^n}\end{aligned}
$$
那么现在我们就可以 O(nlogn) 的时间递归求逆了
多项式对数函数
我们有多项式 $F(x)$ 和 $G(x)$,记 $G \equiv {\ln F} {\pmod{x^n}}$
推式子时间:
$$\begin{aligned}
G &\equiv \ln F &\pmod{x^n} \
G’ &\equiv (\ln F)’ &\pmod{x^n} \
G’ &\equiv (\ln’ F) \ast F’ &\pmod{x^n} \
G’ &\equiv \frac{F’}{F} &\pmod{x^n}
\end{aligned}
$$
我们就可以先把 $G’$ 搞出来,然后再积回去,就是答案啦。
多项式指数函数
我们有多项式 $F(x)$ 和 $A(x)$, 记多项式的对数函数为 $F \equiv e^A \pmod {x^n}$.
对两边分别进行 $\ln$ 运算,得到 $\ln F \equiv A \pmod {x^n}$.
移项,得 $\ln {F} - A {\equiv 0 \pmod {x^n}}$
记 $G(F) = \ln F - A$,有 $G(F) \equiv 0 \pmod{x^n}$
另外。我们有 $G(F_0) \equiv 0 \pmod{x^{\frac{n}{2}}}$。
这时,我们就可以带入牛顿迭代中求解,推式子时间到:
$$
\begin{aligned}
G(F_0) &\equiv 0 \pmod{x^{\frac{n}{2}}} \
F &\equiv F_0 - \frac{G(F_0)}{G’(F_0)} &\pmod{x^n} \
F &\equiv F_0 - F_0 \ast G(F_0) &\pmod{x^n} \
F &\equiv F_0 - F_0(\ln F_0 - A) &\pmod{x^n} \
F &\equiv F_0(A - \ln F_0 + 1) &\pmod{x^n} \
\end{aligned}
$$
又可以递归求解啦
多项式开根
我们有多项式 $F(x)$ 和 $A(x)$,满足 $F^2(x) \equiv A(x) \pmod{x^n}$
要去求多项式 $F(x)$,首先我们要有一个多项式 $H(x)$ 满足 $H^2(x) \equiv A(x) \pmod {x^{\frac{n}{2}}}$
显然,$F^2(x) \equiv A(x) \pmod {x^{\frac{n}{2}}}$ 成立。
记 $G(F) = F^2 - A$.
$$
\begin{aligned}
F^2(x) &\equiv A(x) &\pmod {x^n} \
H^2(x) &\equiv A(x) &\pmod {x^{\frac{n}{2}}} \
H^2 - A &\equiv 0 &\pmod {x^{\frac{n}{2}}} \
G(H) &\equiv 0 &\pmod{x^{\frac{n}{2}}} \
F &\equiv H - \frac{G(H)}{G’(H)} &\pmod{x^n} \
F &\equiv H - \frac{H^2 - A}{2H} &\pmod{x^n} \
F &\equiv \frac{H^2 + A}{2H} &\pmod{x^n}
\end{aligned}
$$
还是递归下去,求个逆元乘起来就好啦。
多项式快速幂
先求 ln,再数乘,最后 exp 即可
多项式全家桶
模板题 :)
[x] P3803 【模板】多项式乘法(FFT)
[ ] P4245 【模板】任意模数多项式乘法
[ ] P4238 【模板】多项式乘法逆
[ ] P4725 【模板】多项式对数函数(多项式 ln)
[ ] P4726 【模板】多项式指数函数(多项式 exp)
[ ] P5205 【模板】多项式开根
[ ] P5245 【模板】多项式快速幂
[ ] P7776 【模板】特征多项式
[ ] P4512 【模板】多项式除法
[ ] P5050 【模板】多项式多点求值
[ ] P5809 【模板】多项式复合逆
[ ] P5373 【模板】多项式复合函数
[ ] P5158 【模板】多项式快速插值
[ ] P5394 【模板】下降幂多项式乘法
[ ] P5277 【模板】多项式开根(加强版)
[ ] P5273 【模板】多项式幂函数(加强版)