数据结构
树
Problem
给定一棵 $n$ 个点的树,每条边有个正整数边权。有 $q$ 次修改操作,每次会修改一条边的边权。
在所有修改之前以及每次修改后,你需要求出有多少个无序点对满足它们之间的最短路径上所有边权的最大公约数 $=1$。
Solution
首先考虑莫比乌斯反演,变为统计 $k∣gcd$ 的点对数量。 对于每个边权,首先去掉重复的质因子,这样它的质因子只有不超过 $c=7$ 个。 那么对于每个 $k$,将边权是 $k$ 的倍数的边取出,用并查集计算答案。 对于修改涉及的边,我们一开始不将它们加入并查集。然后我们枚举 $q+1$ 个时刻,再将这些边加入,统计答案,再删去即可。 时间复杂度 $O(L+(n+q^2)2^c \log n)$
动规篇
Robot and Exit
Problem
现在有 $n$ 个机器人和 $m$ 个出口在一个数轴上,每个机器人和出口都有一个正整数坐标,并且这 $n+m$ 个坐标都互不相同
现在执行若干次操作,每次操作可以是:
将所有机器人的坐标减一
将所有机器人的坐标加一
当一个机器人移到出口的的时候他就会消失,操作将进行直到所有机器人消失
两种操作序列不同,当且仅当存在至少一个机器人在两次操作序列进行完成后从不同的出口消失
给出每个机器人和出口的坐标,求有多少种不同的操作序列,输出方案数对 $10^9+7$ 取模的结果
Solution
首先我们可以不管比最左边 exit 还左边的 robot, 因为它一定从最左边 exit 溜走,对答案没有影响。同理,我们也可以不管比最右边 exit 还右边的 robot.
我们现在单独拎出一个 robot 进行研究。我们发现只有改变他向左或向右的最大值的操作才对这个 robot 有效果。所以我们如果把这个 robot 向左和向右的最大值作为一个平面坐标的两维的话,它的初始值是 $(0, 0)$, 然后不断地向上、向右延伸。
其实所有 robot 的曲线都长一个样.
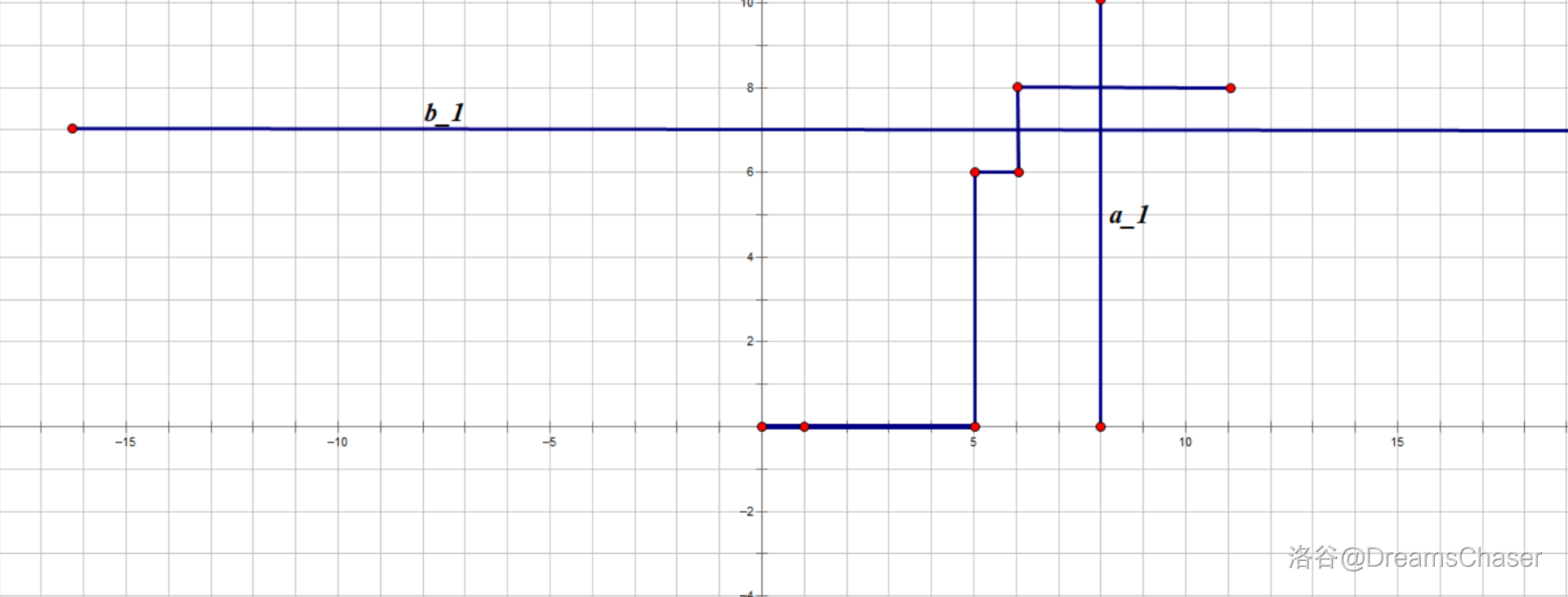
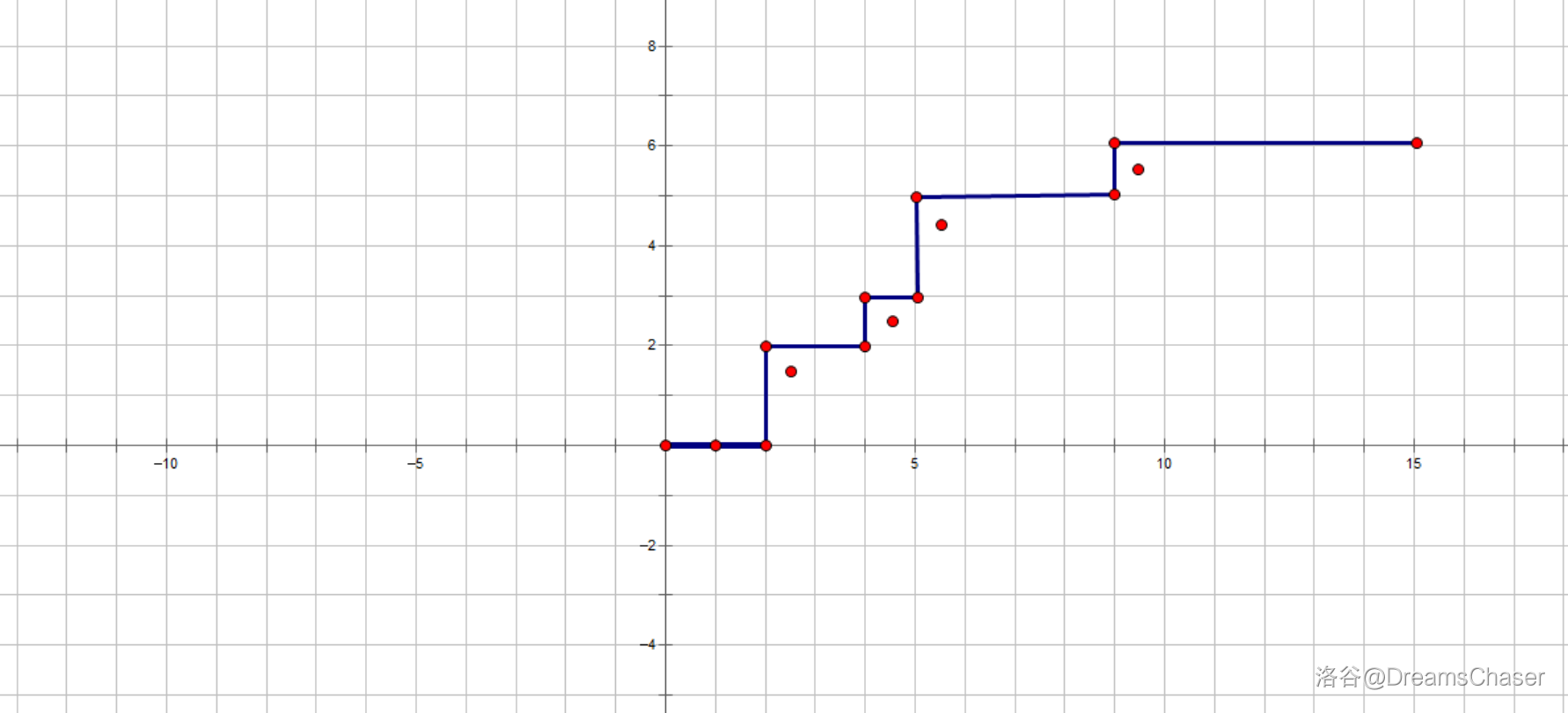
那一个 robot 何时溜走呢?是不是当他碰到了一个 exit 的时候。也就是说,我们设初始时第 $i$ 个 robot 距离离它最近的两边的 exit 的距离分别是 $a_i, b_i$ . 然后这条曲线碰到 $x=a_i$ 或 $y=b_i$ 的时候它就推出历史的舞台了。
而且答案只取决于曲线先碰到 $x=a_i$ 还是 $y=b_i$.
如果将 robot 的左标定义为 $(a_i-0.5, b_i-0.5)$. 那么所有在曲线左上方的 robot 都会从左侧的 exit 溜走,在曲线右下方的 robot 都会从右侧的 exit 溜走。
对于每个从右侧 exit 溜走的 robot 的集合, 容易构造出与之唯一对应的折线:
感性理解一下,就是卡在每个 robot (称为 BR)的直线。反之如果不能这样构造直线,我们也可以保证不存在直线使得这些 robot 都在右下方。
那么方案数就等于这样的直线的个数。令 $f_i$ 表示延伸到第 $i$ 个机器人且这是个 BR.
Satanic Panic
Problem
二维平面上有 $n$ 个点,找出来五个点使得形成一个五角星,求方案数。
Solution
首先五角星可以转化成 $5$ 个点的凸包,然后就可以用计算几何来求解。
怎么判断是否合法呢?可以用叉积,当然也可以通过极角排序保证合法,我用的是后者。
然后就是统计答案,这里用 DP,$f_{i,j,k}$ 表示 $i$ 到 $j$ 有 $k$ 条路径。
对于每条边而言都有 $f_{x_i,y_i,1}=1$,即初始化;
再考虑转移,对于点 $j$,$f_{j,x_i,k}=f_{j,x_i,k}+f_{j,y_i,k-1}$;
最后的答案是 $\sum_{i=1}^{n}f_{i,i,5}$,即所有从自身出发,经过$5$条边又能回到自身的方案数。
Source
其实可以改成六芒星,又是一道题
convex
Problem
给出 $n$ 个点,选择其中若干个点,使得这些点的凸包上点的个数尽量多,保证不存在三个点共线,求最多的点数。
Solution
考虑优化转移,首先出发点可以枚举,不用放在 $dp$ 数组中。
枚举凸包中的最上面的一个点 $T$,然后用 $dp_{i,j}$ 表示最后一个选中的点为 $j$ ,上一个被选中的点为 $i$,凸包上的点数的最大值。
这样的话,相当于我们要从点 $T$ 走一个凸集回到点 $T$。于是 $dp_{i,j}$ 可以从 $dp_{k,i}$ 转移过来,当且仅当 $k->i$ 的极角小于等于 $i->j$ 的极角。(此处的 “极角” 为 atan2() 函数得到的角度)于是我们考虑调整 dp 顺序为:将所有两个点形成的向量按极角排序,以这个顺序来进行 dp,记录一个 $mx_{i}$ 表示当前走到点 $i$ 的凸包点数最大值,每次 $dp_{i,j} = mx_{i} + 1$, 且用 $dp_{i,j}$ 更新 $mx_{j}$。
Source
某次考试题 | 镜像 U243047 convex
数论篇
老凯的疑惑
Fib Gcd
Problem
$$\sum_{i=1}^{n}\sum_{j=1}^{m}\mathrm{Fib}_{\gcd(i,j)}$$
$T,n,m\le10^5$
Solution
抽象出来就是这个式子:
$$\sum_{i=1}^{n}\sum_{j=1}^{m}f(\gcd(i,j))$$
设 $n\ge m$:
$$\begin{aligned}&\sum_{i=1}^{n}\sum_{j=1}^{m}f(\gcd(i,j))\\=&\sum_{d=1}^{n}\sum_{i=1}^{n}\sum_{j=1}^{m}f(d)[\gcd(i,j)=d]\\=&\sum_{d=1}^{n}f(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[\gcd(i,j)=1]\\=&\sum_{d=1}^{n}f(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}\sum_{k|i}\sum_{k|j}\mu(k)\\=&\sum_{d=1}^{n}f(d)\sum_{k=1}^{\lfloor\frac{n}{d}\rfloor}\mu(k)\sum_{k|i,i\le \lfloor\frac{n}{d}\rfloor}\sum_{k|j,j\le \lfloor\frac{m}{d}\rfloor}1\\=&\sum_{d=1}^{n}f(d)\sum_{k=1}^{\lfloor\frac{n}{d}\rfloor}\mu(k)\left\lfloor\frac{n}{dk}\right\rfloor\left\lfloor\frac{m}{dk}\right\rfloor\\=&\sum_{d=1}^{n}\sum_{k=1}^{\lfloor\frac{n}{d}\rfloor}f(d)\mu(k)\left\lfloor\frac{n}{dk}\right\rfloor\left\lfloor\frac{m}{dk}\right\rfloor\\\end{aligned}$$
设 $t=dk$,$g=f\ast\mu$:
$$\sum_{t=1}^{n}g(t)\left\lfloor\frac{n}{t}\right\rfloor\left\lfloor\frac{m}{t}\right\rfloor$$
数论分块,$O(\sqrt n)$ 单次。
Source
一个很经典的模型,只是套上 $\mathrm{Fib}$ 罢了。
--> -->结论篇
flowers
Problem
樱花雨一共持续了 N 秒。每一秒都会有 A 朵樱花飘落。小 Q 细心的记录了每一秒时间
后地上樱花的数目,并将其转换成了二进制。小 Q 想请你统计一下这些二进制数一共有多
少个 1。
Solution
对于这一等差数列 $b+a,b+a\ast 2,b+a\ast 3,…,b+a\ast n$,显然第 $i$ 项与第 $2^k+i$ 项在第 $k$ 位上的数字相同。
于是,可以将原数列按位拆成循环节统计。
Source
某道考试题。
Range XOR
原题:ARC133D
对于 $0≤k$,我们定义 $wk=0⊕1⊕⋯⊕(k−1)$。
我们想要计算满足 $L≤i<j≤R+1$ 并且 $wi⊕wj=V$ 的数对 $(i,j)$。
经过一点变换, 问题变成了寻找数对 (i,j) 满足 $0≤i<A,0≤j<B,wi⊕wj=V$.
把它们模4的结果进行分类,我们可以得到:
- $w_{4x}=x$
- $w_{4x+1}=1$
- $w_{4x+2}=x+1$
- $w_{4x+3}=0$
因此,我们只需确定 $i$ 和 $j$ 模 $4$ 的余数,一共 $16$ 种情况。但是比较难处理的只有 $(0,0),(0,2),(2,0),(2,2)$ 四种情况,其余情况要么可以确定一个端点的位置,要么形如等差数列,均可快速求得。
这四种情况本质是一样的,给定区间 $[l−1,r]$ ,从区间中抽取两个不相等的数 $a,b$ ,求 $a⊕b=V$ 的对数。
可以用数位 dp 解决,$f[i][j][k]$ 表示还有 $i$ 位,第一个数是否卡上界,第二个数是否卡上界的方案数。然后我们就做完了。